Co jsme se ve škole neučili ...
doc. MUDr. Pavel Kasal, CSc., Mgr. Marie Hladíková (Ústav lékařské informatiky 2. LF UK)
Skoro každý lékař se občas dostává do role statistika amatéra. Vše většinou začíná tím, že je nucen zpracovat svůj materiál pod tlakem okolností (blíží se termín přednášky, závěrečné grantové zprávy a pod.).
Samostatné vyhodnocení výsledků na počítači včetně příslušných grafů je sice lákavé a někdy vzhledem k okolnostem i nezbytné, statistických problémů je totiž ve zdravotnictví mnohem více než statistiků. Na druhé straně se však takový lékař ocitá na vratké půdě, na kterou není dostatečně teoreticky připraven. V dané souvislosti se nabízí možnost prostudovat statistickou literaturu, což je spojeno s nejrůznějšími pocity:
Pro uvedené situace lze uvést několik praktických rad z kuchařky statistické kuchyně:
Rozdělení četností
1. Grafické vyjádření distribuce četnosti
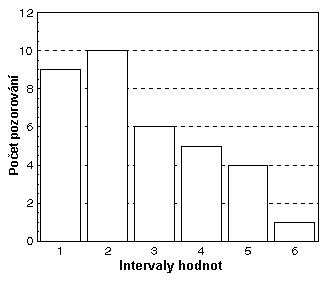
Velmi výhodným prvním krokem je grafické znázornění našeho souboru, jehož vlastnosti nám vyjadřuje histogram četnosti. Jedná se o graf, kde se vynášejí na osu x intervaly sledované hodnoty, na osu y pak počet pozorování pro daný interval (Obr.1). Problém, který činní potíže a kde se nejčastěji chybuje je právě stanovení tohoto intervalu. Při menším počtu hodnot se totiž volbou intervalů histogram natolik mění, že jsme v pokušení modifikovat intervaly tak dlouho, dokud histogram nepřipomíná Gaussovu křivku.
Je proto dobré přidržet se některého pravidla pro volbu počtu intervalů - např.: Konkrétně tedy kolik sloupců histogramu v rámci grafického vyjádření vlastně zvolit. Hledaný počet intervalů závisí obecně na počtu pozorování a lze jej odvodit podle následujících vzorců:
log - symbol pro dekadický logaritmus (funkce log je na každé kvalitnější kalkulačce).
Příklad: Pro soubor o 35 jedincích činí počet potřebných intervalů 1+(3.3*1.51)=6.
2. Ověření normality rozdělení
Před prováděním statistických výpočtů musíme především ověřit, jestli má náš soubor normální rozdělení či nikoliv. Pokud totiž normální nemá, je nutno testovat hypotézy tzv. neparametrickými testy a zejména nelze provádět v těchto případech již ani výpočet aritmetického průměru a směrodatné odchylky!!
Takovýto postup by totiž mohl být ze statistického hlediska značně zkreslující. Uvedené parametry je zde nutno nahradit kupř. mediánem, kvantily apod. Pro normální rozdělení svědčí zhruba distribuce četnosti, jež vytváří přibližný tvar Gaussovy křivky. U histogramu z většího množství pozorování může zkušené oko tento tvar odhadnout (maximum hodnot uprostřed minimum extrémních hodnot, stupňovitý přechod na obě strany). Často jsou však histogramy dosti nepravidelné a pro získání seriózních výsledků je navíc stejně nutno ověřit normalitu výpočtem (kupř. Kolmogorov-Smirnovův test). Statistik amatér si však může orientačně ověřit normalitu, následujícími pomocnými prostředky:
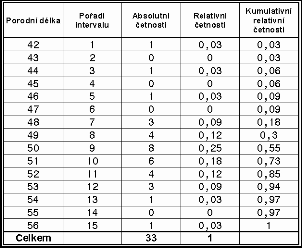
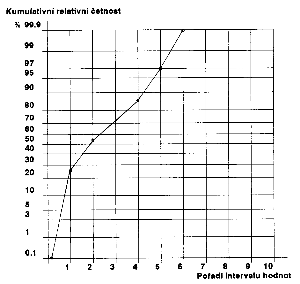
Vizuální posouzení umožňuje použití pravděpodobnostní stupnice (Obr.2). Ta je zkonstruovaná tak, že distribuční křivku normálního rozdělení převádí na přímku.
Postup: Na osu x nanášíme pořadí intervalu zjištěných hodnot, na osu y relativní kumulovanou četnost, tj. součet % všech dosavadních hodnot (příklad viz tabulka). Pokud se jedná o normální rozdělení, představuje vzniklý graf přímku. Na Obr.2 vidíme křivku rozdělení, která se od normálního liší. Jedná se o rozdělení levostranně asymetrické, zobrazené na uvedeném histogramu (Obr.1). Může se ovšem stát, že histogram naznačuje přítomnost více vrcholů. Pokud zjistíme takovéto dvou- nebo vícevrcholové rozdělení (tzv. bimodální křivka), vzniká závažný důvod pro hlubší zamyšlení nad zadáním celé statistické úlohy. Jedná se totiž o signál, že může být soubor nehomo- genní a že je tedy zapotřebí vytvořit soubory nové, aby nedošlo k onomu pověstnému smíchání jablek a hrušek dohromady.
Obsah čísla 3/95